Spatial Angular Velocity vs Body Frame Angular Velocity

Research, Research Blog 4 Minutes

A while ago I had written about IMU pre-integration (blog-link). Particularly, I had played around with the inertial measurements data (IMU data) and tried to dig a bit deeper on what exactly does the IMU measurements mean. So the conclusion was that the IMU measure the body frame angular velocity and body-frame angular velocity (and not the world frame angular velocities and linear accelerations). This subtle difference is sometimes hard to imagine.

Imagine a car moving and you are in a car and it is at a constant speed. You look at the speedometer and it says 60 kmph. This figure is the car’s linear velocity with respect to the world aka the spacial frame velocity of the car. The RPM of a car engine is a body frame measurement. The body frame measurements is not super intuitive to imagine in my opinion.

In this post, I will try to clarify the difference between the angular velocity when represented in body frame vs angular velocity when represented in spatial-frame (or the world-frame). Particularly, the situation is that we are trying to simulate an imu and want to synthetically generate imu measurements (without noise).

Conclusion

Given that the position of a point q on the rotating object, b varies as a function of rotational matrix R(t). The rotation matrix can be composed with, for example, Euler angles. The angles are represented in the spatial frame (world-frame, w) and as a function of time. Thus R(t) is the instantaneous rotation of the point q with respect to the world ie. ^{w}R(t)_b . We shall use just R(t) for concise notations. \hat {E} is the hat operator. and {E}^{V} is the v-operator, the inverse operator of the hat operator.

The spatial frame angular velocity is: \hat \omega(t) := \dot R(t) . R^T(t)

The body frame angular velocity is: \hat \Omega(t) := R^T(t) . \dot R(t)

How can this be proved?

As mentioned previously, the situation is that we can vary the angles independently and generate IMU measurements. Recall that we are interested in angular velocity in body frame (^b\Omega_{wb}). As a first step, lets try to understand how to generate angular velocities in spatial-frame (world-frame, ie. ^w\omega_{wb}). Let x_0 be the initial position of point q, in world-frame.

Time derivative of position in spatial co-ordinates

x(t) = R(t) . x_0 …(1)
…taking time derivatives on both sides,
\dot x(t) = \dot R(t) . x_0
using equation(1) and the fact that rotational matrix’s inverse is its transpose,
\dot x(t) = \dot R(t) . R(t)^T . x(t) …(2)

The Matrix, \dot R(t) . R(t)^T is skew-symmetric

Next we want to show that \dot R(t) . R(t)^T is a skew-symmetric matrix. We want to prove that because, in that case the eq(2) can be viewed as a cross product. Recall that for a matrix A to be skew-symmetric its transpose has to be the negative of it. For a skew-symmetric matrix A, A + A^T = 0. Following is the proof for it,

R(t) . R(t)^T = I_3
time derivative on both side and using the chain rule,
\dot R(t) . R(t) + R(t) . \dot R(t)^T = 0_3
\dot R(t) . R(t)^T = - R(t) . \dot R(t)^T
using the property, (A . B)^T = B^T . A^T
\dot R(t) . R(t)^T = - [ ( \dot R(t)^T )^T . R(t)^T ]^T
\dot R(t) . R(t)^T = - [ \dot R(t) . R(t)^T ]^T

This proves that the matrix \dot R(t) . R(t)^T is skew-symmetric.

Angular Velocity in Spatial Frame

From basic definition, the Linear velocity is cross product between the angular velocity and position vector (all represented in world-frame). Also recall that cross product can be represented with a hat-operator.

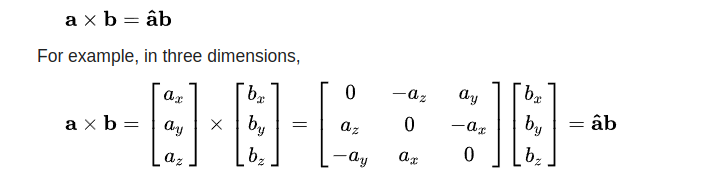
Continuing with Eq(2), it is clear that world-frame angular velocity is the V-operator of \dot R(t) . R(t)^T. The V-operator is the inverse operator of the hat-operator.

\dot x(t) = \dot R(t) . R(t)^T . x(t)
\dot x(t) = [ \dot R(t) . R(t)^T ]^V \times x(t)
Comparing with the definition of angular velocity, \dot x(t) = \omega(t) \times x(t). Thus the first conclusion:

\hat \omega(t) := \dot R(t) . R^T(t) …(a)

Angular Velocity in Body Frame

The body frame angular velocity (\Omega(t) is the transformation of \omega(t) with the inverse of R(t), ie:

\Omega(t) = ( R(t) )^{-1} . \omega(t)
\Omega(t) = R(t)^T . \omega(t) …(3)

Let us refer to the body frame position of point q as X(t) := ^{b}X(t).
^{b}X(t) = ^bR(t)_w . ^wx(t) .
In concise notations,
X(t) = R(t)^T x(t) …(4)

Taking the cross product of Eq(3) and Eq(4) we get,
\Omega(t) \times X(t) = R(t)^T . \omega(t) \times R(t)^T x(t)
\Omega(t) \times X(t) = R(t)^T ( \omega(t) \times x(t) )
Using the 1st conclusion ie. eq(a) and the basic definition of cross product with hat-operator,
\hat \Omega(t) . X(t) = R(t)^T . \hat \omega(t) . x(t)
\hat \Omega(t) . X(t) = R(t)^T . \dot R(t) . R^T(t) . x(t)
\hat \Omega(t) . X(t) = R(t)^T . \dot R(t) . X(t)
so we conclude,

\hat \Omega(t) = R(t)^T . \dot R(t) ….(b)

This is exactly the 2nd conclusion. I hope the confused future me or a reader looking for an explanation on body frame angular velocity and world frame angular velocity might find this helpful.

References

Unknown's avatar

Published by kusemanohar

Published

Leave a comment